＜例題＞直角三角形ＡＢＣ の内心を Ｉ とし、Ｉ から３辺に垂線を降ろし、垂線と辺に接する
図のよう３つの円と△ＡＢＣの内接円がある。中心が Ｐ、Ｑ の円の半径を ９，８ と
するとき、中心が Ｒ の円の半径を求めよ。(和算問題を改題、元の問題は下にあり）
＜解答＞△ＡＢＣ の内接円の半径を ｒ とすると、
条件より、(ＱＰ)Ｓ＝(ＱＬ＋ＬＡ＋ＡＫ＋ＫＰ)Ｓ
＝(ＱＬ)Ｓ＋(ＬＡ)Ｓ＋(ＡＫ)Ｓ＋(ＫＰ)Ｓ
＋２(ＱＬ・ＬＡ)＋２(ＱＬ・ＡＫ)＋２(ＱＬ・ＫＰ)
＋２(ＬＡ・ＡＫ)＋２(ＬＡ・ＫＰ)
＋２(ＡＫ・ＫＰ)
＝(ＱＬ)Ｓ＋(ＬＡ)Ｓ＋(ＡＫ)Ｓ＋(ＫＰ)Ｓ
＋２(ＱＬ・ＡＫ)＋２(ＬＡ・ＫＰ)
(９＋８)２＋(９−８)２
＝(８)２＋(８＋ｒ)２＋(ｒ＋９)２＋(９)２
＋２{−８×(ｒ＋９)}＋２{−(ｒ＋８)×９}
９２＋２×９×８＋８２＋９２−２×９×８＋８２
＝８２＋８２＋１６ｒ＋ｒ２＋ｒ２＋１８ｒ＋９２＋９２
−１６ｒ−１４４−１８ｒ−１４４
０＝ｒ２＋ｒ２−１４４−１４４
＝２ｒ２−２８８
＝ｒ２−１４４
１４４＝ｒ２
ｒ＝１２
ｒ/２＝６・・・・・・・・（答）
＜例題＞直角三角形ＡＢＣ の中に図のよう３つの円と △ＡＢＣの内接円がある。大円、中円の
の半径を ９，８ とするとき、小円の半径を求めよ。
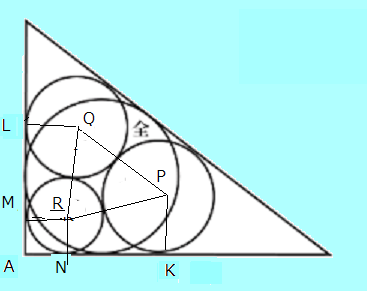＜解答＞中心が Ｒ の円の半径を ｒ とすると、
条件より、(ＫＮ)Ｓ＝(ｒ＋９)Ｓ−(ｒ−９)Ｓ＝４ｒ×９
|ＫＮ|＝６×ｒ１/２
(ＬＭ)Ｓ＝(ｒ＋８)Ｓ−(ｒ−８)Ｓ＝４ｒ×８
|ＬＭ|＝４×(２ｒ)１/２
上の式より、
(ＱＰ)Ｓ＝(ＱＬ＋ＬＡ＋ＡＫ＋ＫＰ)Ｓ
＝(ＱＬ)Ｓ＋(ＬＡ)Ｓ＋(ＡＫ)Ｓ＋(ＫＰ)Ｓ
＋２(ＱＬ・ＬＡ)＋２(ＱＬ・ＡＫ)＋２(ＱＬ・ＫＰ)
＋２(ＬＡ・ＡＫ)＋２(ＬＡ・ＫＰ)
＋２(ＡＫ・ＫＰ)
＝(ＱＬ)Ｓ＋(ＬＡ)Ｓ＋(ＡＫ)Ｓ＋(ＫＰ)Ｓ
＋２(ＱＬ・ＡＫ)＋２(ＬＡ・ＫＰ)
(９＋８)２＝(８)２＋(４×(２ｒ)１/２＋ｒ)２＋(６×ｒ１/２＋ｒ)２＋(９)２
＋２{−８×(６ｒ１/２＋ｒ)}＋２{−(４×(２ｒ)１/２＋ｒ)×９}
１４４＝(４×(２ｒ)１/２＋ｒ)２＋(６ｒ１/２＋ｒ)２
＋２{−８×(６×ｒ１/２＋ｒ)}＋２{−(４×(２ｒ)１/２＋ｒ)×９}
＝２ｒ２＋{８×(２)１/２＋１２}ｒ３/２
＋{３４}ｒ＋{−７２×(２)１/２ー９６}ｒ１/２
０＝２ｒ２＋{８×(２)１/２＋１２)１/２}ｒ３/２
＋{３４}ｒ＋{−７２×(２)１/２ー９６}ｒ１/２−１４４
＝ｒ２＋{４×(２)１/２＋６}ｒ３/２
＋{１７}ｒ＋{−３６×(２)１/２ー４８}ｒ１/２−７２
ｆ(ｒ)＝ｒ２＋２{２×(２)１/２＋３}ｒ３/２
＋{１７}ｒ−１２{３×(２)１/２＋４}ｒ１/２−７２ とおく。
上の例題より、ｆ(６)≒０
ｆ(６)＝６２＋{４×(２)１/２＋６}(６)３/２
＋{１７}(６)＋{−３６×(２)１/２ー４８}６１/２−７２
＝・・・・・・
ｆ(７)＝・・・・・・
・・・・・・
・・・・・・
ｆ(６.１)＝・・・・
・・・・・・
・・・・・・
ｆ(６.０９)＝・・・・
準 備 中
これが既存の数学の範囲で解いた秀才の解答です。
ここには優秀なスタッフをそろえてＨＰが運営されているようで、個人が制作
するＨＰとは段が違います。それ故に相当に難しく・・・、平均的な生徒には手
が届きそうにありません。これは「頭が悪い者は諦めなさい」と言っているよう
なものです。まぁ・・・、そも、そも、これは江戸のカミソリ頭脳脳の発想の原
点ですから、和算の問題を解けば、こうなるのは、ある程度「止む無し」なので
しょう。
数学の解答は己の実力を見せびらかすところではありません。「俺が作った問
題をやって見ろ、出来ないだろう・・・」 こんなことよりも、落ちこぼれを一
人でも少なく！！！
幾何学の答えは、自然数に始まり、整数、有理数、無理数、更には、π、ｅ，
超越数、と必要に応じて、どんどん追加していっても一向に構いませんが、これ
では切りがありません。それでもって全ての答えを表すことは出来ません。こん
な問題に出あったら、与えられた問題に可能な限り近く、かつ、答えが有理数で
表される問題に作り変え、これを解いて、その答えを足場にして、問題の答えを
挟む微分演算の数（ａｎ，ｂｎ）を作り、これを答えにします。こうして置かな
いことには、幾何学の全ての問題に対応出来ません。
そもそも、微分演算の数は、その名前の通り、微分積分構築のために、当ＨＰ
で、実数に代わるものとして作った数なのですが、それ以外の分野に使っても罰
が当たらんでしょう。と言うよりも、微積分の誕生前に微分演算の数(実数)をあ
らかじめ作っておいて、それが十分に成熟するのを待って、これを使い、数学が
微積分を創造していたならば、あのどうしようもない「無限、極限」への迷路に
陥ることなく、微積分の発展がスム−スだっただろうと考えられます。まぁ、そ
んなことは、出来上がった数学を眺めた三、四流の数学者か、あるいは、創造出
来る能力を持たないないが、数学者のような顔をしたい評論家が考える「机上の
空論」であって、無茶苦茶と言うものです。
イエ、イエ、そんなんことはありません。江戸の昔、和算にはそれがありまし
た。和算家は微積分の準備をしていたのであったが、微積分は誕生しませんでし
た。
その理由は、和算学者が「天体の運行から、地上の運動の法則」へと、目を向
けられなかったからでしょう。これが和算と洋算の決定的な差となったと考えら
れます。「和算は当時の世界最高水準であった？？？」 こんな説があるそうな
ぁ・・・？？？ これは嘘八百でしょう。明治政府が和算を捨て、洋算を採用し
たのは賢明で、これが今日の日本を作ったのは確かである。
リンゴが木から落ちるのは当たりまえ・・・？
これでは微積分は誕生しません。
まぁ・・・、ねぇ・・・、十分な準備をしなくとも、微分積分を創造し得たの
は、西洋の数学者が偉大であったことの証です。さりながら・・・、同時に大変
な欠陥も伴っていまして。似たようなことは他の分野にもあります。その代表は
虚数「Ｉ」、ユークリット幾何学の「公理｝です。どうやら・・・、西洋の天才
数学者は、大地と足の裏の接触部分が鈍感だったようで、最近のナノテクノロジ
ーの分野に足を踏み込むと「力不足」になることが予想されます。
| 
