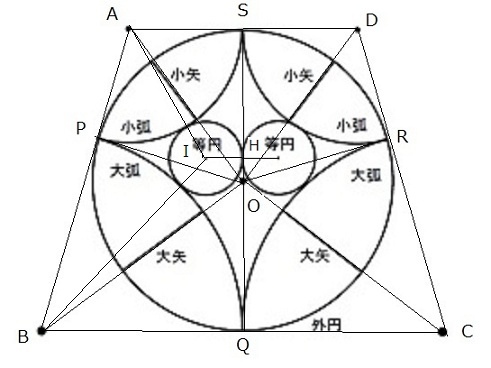
 <例題>下の図のように、等脚台形に外円が内接している。外円を4つ弧(中心は台形の頂点)に
よって5つの部分に分け、中央部分に等円が2つ内接している。外円と大弧の間の中心
線(大矢)の長さが 49寸、外円と小弧の間の中心線(小矢)の長さが 36.75寸 のと
き、等円の直径を求めよ。
<解答>大円の半径を r、等円の半径を s、AP=AS=x、BP=BQ=y とし、点は下
の図にあるものとする。
<例題>下の図のように、等脚台形に外円が内接している。外円を4つ弧(中心は台形の頂点)に
よって5つの部分に分け、中央部分に等円が2つ内接している。外円と大弧の間の中心
線(大矢)の長さが 49寸、外円と小弧の間の中心線(小矢)の長さが 36.75寸 のと
き、等円の直径を求めよ。
<解答>大円の半径を r、等円の半径を s、AP=AS=x、BP=BQ=y とし、点は下
の図にあるものとする。
 条件より、(OA)S=(OP+PA)S=(OP)S+2(OP・PA)+(PA)S
=(OP)S+2(0)+(PA)S
=(OP)S+(PA)S
(x+r−a)2=x2+r2・・・・・・・・・・・・・・・・・・・・・(1)
同様に、(y+r−b)2=y2+r2・・・・・・・・・・・・・・・・・・・・・(2)
(x+r−a)2+(y+r−b)2=(x+y)2・・・・・・・・・・・・・(3)
(1)より、x2+r2+a2+2xr−2xa−2ra=x2+r2
a2+2xr−2xa−2ra=0
x=(a/2)(2r−a)/(r−a)
(2)より、同様にして、 y=(b/2)(2r−b)/(r−b)
(1)+(2)−(3) 0=x2+r2+y2+r2−(x+y)2
=2r2−2xy
=r2−xy・・・・・・・・・・・・・・・・・・・・(4)
(4) に x=(a/2)(2r−a)/(r−a)、y=(b/2)(2r−b)/(r−b) を代入、
0=r2−{(a/2)(2r−a)/(r−a)}{(b/2)(2r−b)/(r−b)}
=4r2(r−a)(r−b)−ab(2r−a)(2r−b)
=4r2{r2−(a+b)r+ab}−ab{4r2−2(a+b)r+ab}
=4r2{r2−(a+b)r}−ab{−2(a+b)r+ab}
=4r4−4(a+b)r3+2ab(a+b)r−(ab)2
={2r2−ab}{2r2−2(a+b)r+ab}
={2r2−2(a+b)r+ab} ∵ 2r2−ab≠0
r={(a+b)+(a2+b2)1/2}/2 ∵ r>a+b
={(49+36.75+61.25}/2=73.5
2r=147
r2=5402.25
上の式より、x=(a/2)(2r−a)/(r−a)
=(49/2)(147−49)/(73.5−49)
=98
y=(b/2)(2r−b)/(r−b)
=(36.75/2)(147−36.75)/(73.5−36.75)
=55.125
x+y=98+55.125=153.125
条件より、(IA)S=(IH+HS+SA)S
=(IH)S+(HS)S+(SA)S
+2(IH・HS)+2(IH・SA)+2(HS・SA)
=(IH)S+(HS)S+(SA)S
+2(0)+2(IH・SA)+2(0)
=(IH)S+(HS)S+(SA)S+2(IH・SA)
(x+s)2=(s)S+(HS)S+(x)S+2(−sx)
4xs=(HS)S
2(xs)1/2=|SH|
同様に、2(ys)1/2=|HQ|
条件より、|SH|+|HQ|=|SQ|
上の式より、2{xs}1/2+2{ys}1/2=2r
{xs}1/2+{ys}1/2=r
s1/2=r/(x1/2+y1/2)
s=r2/(x+2x1/2y1/2+y)
=r2/(x+y+2r)
=5402.25/(153.125+147)
=18
2s=36寸・・・・・・・・・・・・・・・(答)
条件より、(OA)S=(OP+PA)S=(OP)S+2(OP・PA)+(PA)S
=(OP)S+2(0)+(PA)S
=(OP)S+(PA)S
(x+r−a)2=x2+r2・・・・・・・・・・・・・・・・・・・・・(1)
同様に、(y+r−b)2=y2+r2・・・・・・・・・・・・・・・・・・・・・(2)
(x+r−a)2+(y+r−b)2=(x+y)2・・・・・・・・・・・・・(3)
(1)より、x2+r2+a2+2xr−2xa−2ra=x2+r2
a2+2xr−2xa−2ra=0
x=(a/2)(2r−a)/(r−a)
(2)より、同様にして、 y=(b/2)(2r−b)/(r−b)
(1)+(2)−(3) 0=x2+r2+y2+r2−(x+y)2
=2r2−2xy
=r2−xy・・・・・・・・・・・・・・・・・・・・(4)
(4) に x=(a/2)(2r−a)/(r−a)、y=(b/2)(2r−b)/(r−b) を代入、
0=r2−{(a/2)(2r−a)/(r−a)}{(b/2)(2r−b)/(r−b)}
=4r2(r−a)(r−b)−ab(2r−a)(2r−b)
=4r2{r2−(a+b)r+ab}−ab{4r2−2(a+b)r+ab}
=4r2{r2−(a+b)r}−ab{−2(a+b)r+ab}
=4r4−4(a+b)r3+2ab(a+b)r−(ab)2
={2r2−ab}{2r2−2(a+b)r+ab}
={2r2−2(a+b)r+ab} ∵ 2r2−ab≠0
r={(a+b)+(a2+b2)1/2}/2 ∵ r>a+b
={(49+36.75+61.25}/2=73.5
2r=147
r2=5402.25
上の式より、x=(a/2)(2r−a)/(r−a)
=(49/2)(147−49)/(73.5−49)
=98
y=(b/2)(2r−b)/(r−b)
=(36.75/2)(147−36.75)/(73.5−36.75)
=55.125
x+y=98+55.125=153.125
条件より、(IA)S=(IH+HS+SA)S
=(IH)S+(HS)S+(SA)S
+2(IH・HS)+2(IH・SA)+2(HS・SA)
=(IH)S+(HS)S+(SA)S
+2(0)+2(IH・SA)+2(0)
=(IH)S+(HS)S+(SA)S+2(IH・SA)
(x+s)2=(s)S+(HS)S+(x)S+2(−sx)
4xs=(HS)S
2(xs)1/2=|SH|
同様に、2(ys)1/2=|HQ|
条件より、|SH|+|HQ|=|SQ|
上の式より、2{xs}1/2+2{ys}1/2=2r
{xs}1/2+{ys}1/2=r
s1/2=r/(x1/2+y1/2)
s=r2/(x+2x1/2y1/2+y)
=r2/(x+y+2r)
=5402.25/(153.125+147)
=18
2s=36寸・・・・・・・・・・・・・・・(答)
| 





 ここをクリックして,誤り,ご意見,ご質問を送って下ださい。
ここをクリックして,誤り,ご意見,ご質問を送って下ださい。









 ここをクリックして,誤り,ご意見,ご質問を送って下ださい。
ここをクリックして,誤り,ご意見,ご質問を送って下ださい。


